|
|
||||||||||||
 |
||||||||||||
 |
||||||||||||
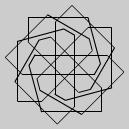
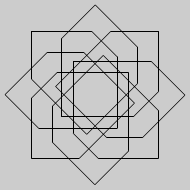
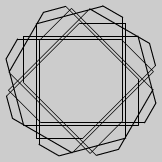
Recursive ReturnsClick here to try using Recursive Returns for yourself. Keep reading to learn more about the principles behind it and how to use it. Once you understand this, you can try the challenge and learn how problem solving can work. OverviewA Recursive action is one that keeps occurring in a repetitive fashion. In this interactive activity you can create a dazzling array of patterns by having a simple action repeated any number of times. This activity is like a simplified, visual version of the LOGO drawing language. ExamplesBelow are some examples of what you can do in the Recursive Returns activity:
ActivityChange the values in the following activity to make different patterns. If you want to reset the activity to the original settings, hit the “Refresh” or “Reload” button in your Internet browser.
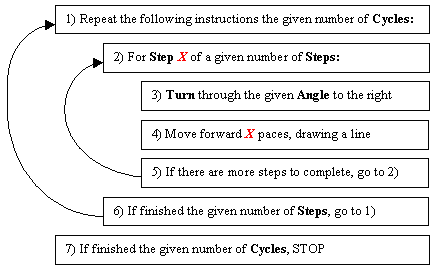
Example (how the activity above starts)When you start this activity in Normal mode, the following recursive process takes place:
Try changing the “Angle to Turn” to 89 degrees - it will help you see the example above. Details of How this Activity WorksNormal Mode:This activity uses the following recursive process:
Expert Mode:Now, for each Step you can change the Angle and Number of Paces separately and repeat for a given number of Cycles. The Challenge: Predictable PatternsIn the example above, after a total of 24 paces, you end up in exactly the same place as where you started! Can you discover the conditions under which you will end up in the same place as where you started? Test your theory by making some predictions and seeing if they work in the activity above. When you get the hang of normal mode, try expert mode (click the tab in the top-right hand corner of the activity). Be sure to try changing all variable, including “Angle”. Does your theory above still hold true? Problem SolvingThe process you have used above is a good example of how to problem solve. In this case, you can think of problem solving as:
However, remember that even though you can prove a theory wrong, you can never prove a theory right - there could always be a condition you did not think of that makes your predictions fail. Therefore, the best you can ever say is that your theory holds under a given set or a given range of conditions. |
|
::Home:: ::About Us:: ::Solutions:: ::Video Services:: ::GamED:: ::X-Stream:: ::Imaginality:: ::Contracting:: ::Resources:: ::Search:: |
|
|
||||||||||||||||